数学实践的闪存卡游戏介绍
数学实践的闪存卡简介
数学实践的闪存卡好玩吗?数学实践的闪存卡游戏介绍
导读:期待已久的热门手游数学实践的闪存卡火爆来袭啦!这款手机游戏吸引了大批游戏玩家的的关注,有很多玩家都在问九游小编数学实践的闪存卡好玩吗?想知道这款手游怎么样?今天小编就来说一下数学实践的闪存卡游戏介绍,带各位玩家详细了解一下这款手机游戏的所有玩法特点系统分析介绍,你就会知道数学实践的闪存卡究竟怎么样,好不好玩了!
数学实践的闪存卡

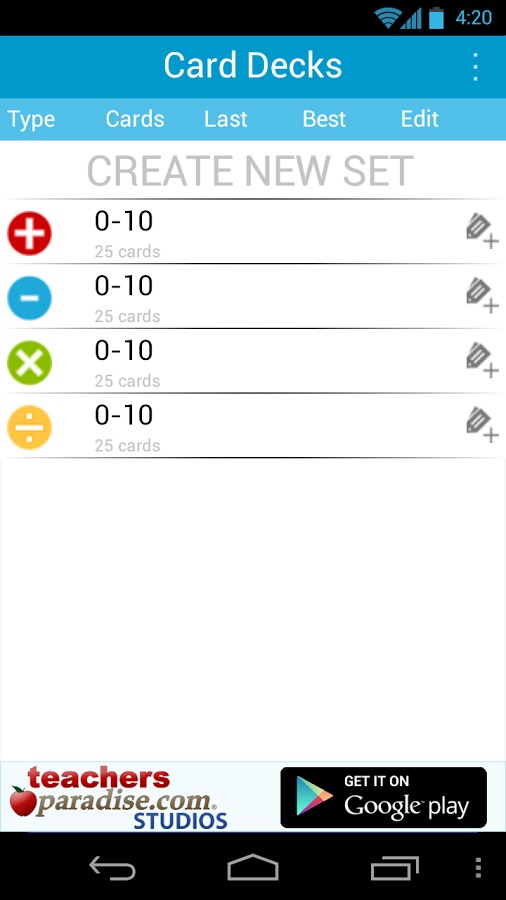
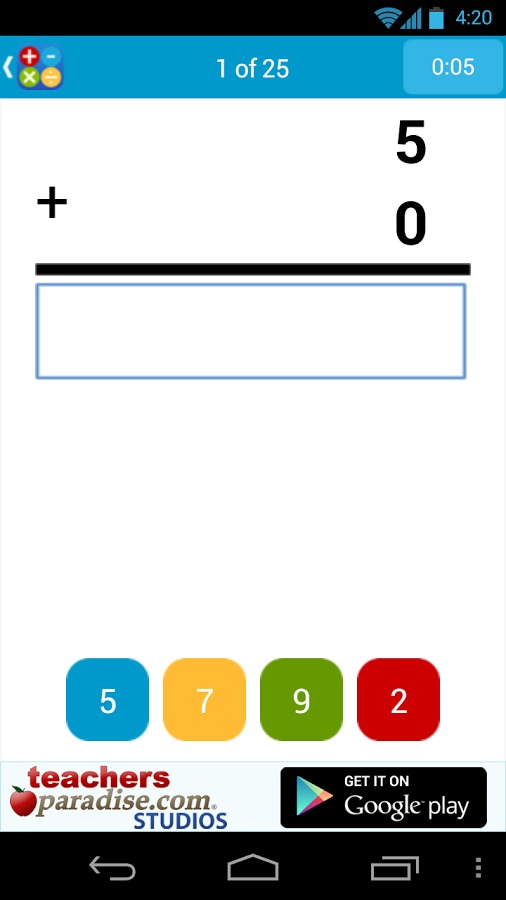
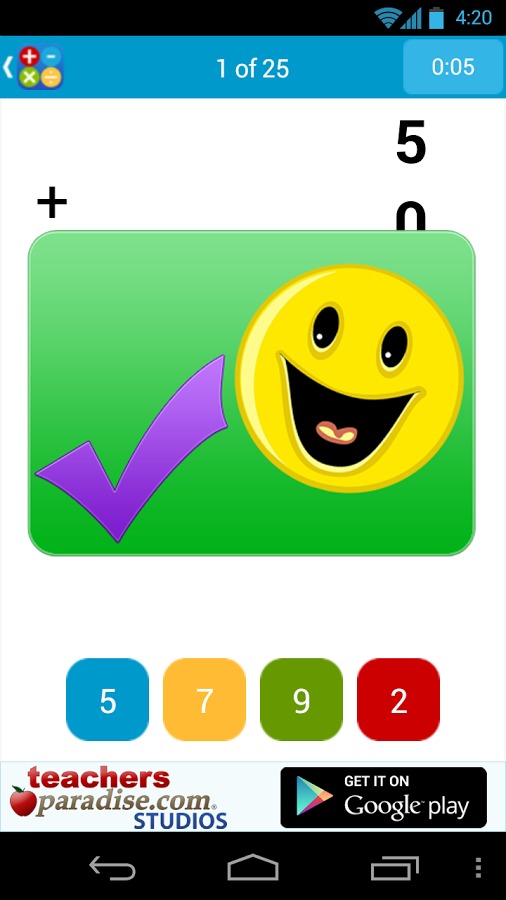
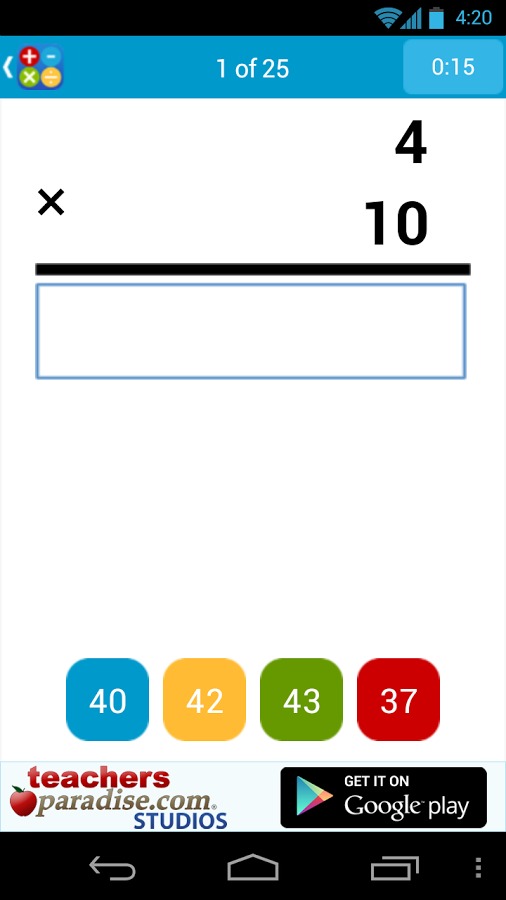
看了上边的数学实践的闪存卡游戏介绍,各位玩家是否都了解了这款手游全部玩法特点系统分析介绍,知道数学实践的闪存卡怎么样,好不好玩呢!
数学实践的闪存卡游戏截图







大家都在看-热门推荐
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
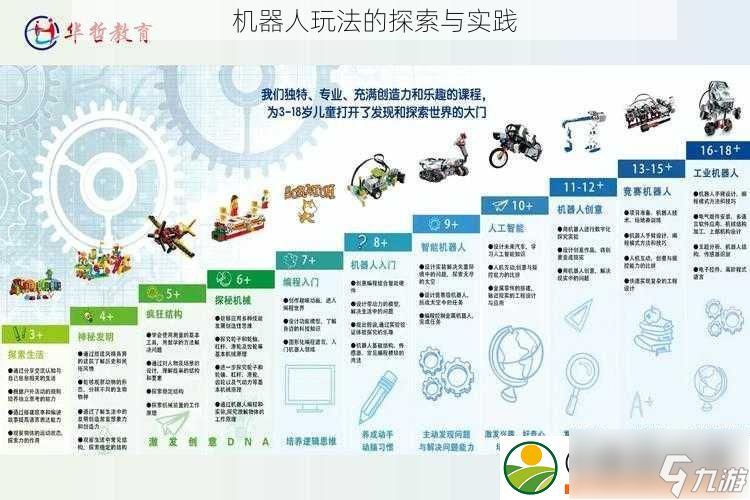
机器人玩法的探索与实践
随着科技的不断发展,机器人玩法已经成为了现代社会中越来越热门的话题。从工业制造到医疗服务,再到军事领域,机器人的身影越来越广泛。而对于普通人来说,了解机器人玩法不仅可以增加生活的乐趣,还可以为未来的职业发展打下坚实的基础。本文将从机器人玩法的探索与实践的角度出发,介绍机器人玩法的相关知识,让读者更深入地了解机器人玩法的魅力。
机器人玩法的探索
机器人玩法是个涉及多个领域的交叉学科,其中包括机械工程电子工程计算机科学等多个领域。在机器人玩法的探索中,我们需要了解机器人的基本原理机械结构控制系统等方面的知识。还需要了解不同领域机器人的应用场景技术难点以及解决方案。
在探索机器人玩法的过程中,我们可以通过阅读相关书籍参加专业培训课程参观机器人展览等方式来获取更多的知识和信息。我们还可以关注些机器人相关的社交媒体账号论坛等,了解最新的技术进展行业新闻等。
机器人玩法的实践
机器人玩法的实践是指通过实际操作来了解机器人的性能功能等方面的知识。在实践中,我们可以根据机器人的类型用途等来选择不同的实践方式。例如,对于工业机器人,我们可以通过观察其操作流程了解其工作效率等方式来进行实践。对于服务机器人,我们可以体验其提供的服务了解其交互能力等方面的知识。
在机器人玩法的实践中,我们需要注意安全。由于机器人具有定的危险性,因此在进行实践时应该采取必要的安全措施,如穿戴防护装备设置安全距离等。我们还需要注意对机器人的维护保养等方面的,以确保机器人的正常运行和使用寿命。
机器人玩法的应用
机器人玩法在各个领域都有着广泛的应用。例如,在工业制造领域,机器人可以完成生产线上的重复性工作提高工作效率和产品质量。在医疗服务领域,机器人可以协助医生进行手术操作减轻医护人员的工作负担等。在军事领域,机器人可以执行侦察搜救等危险任务保护士兵的生命安全等。
除了以上领域,机器人玩法还可以应用于服务行业娱乐行业等。例如,服务机器人可以为客户提供自主点餐送餐等服务,提高餐厅的效率和客户体验。娱乐机器人则可以为客户提供游戏跳舞等娱乐项目,增加客户的乐趣和体验。
读者可以更深入地了解机器人玩法的相关知识。从探索机器人玩法的基本原理机械结构控制系统等方面入手,到实践机器人玩法的性能功能等方面,最后了解机器人玩法在各个领域的应用场景技术难点以及解决方案。希望读者能够通过本文的学习,更好地掌握机器人玩法的相关知识,为未来的职业发展打下坚实的基础。也期望读者能够关注机器人玩法的最新技术进展和行业新闻,以便更好地把握这个领域的机遇和挑战。
2023数学游戏大闯关 好玩的数学游戏推荐
在我们的日常生活中离不开数学,网上也有很多关于数学的游戏,那么2023数学游戏大闯关有哪些?在游戏中可以帮助玩家开发大脑的思维,还有不同的关卡,可以在这里不断的闯关,下面就是今天小编分享给大家好玩的数学游戏推荐。
1、《数独大全》

这是一款适合任何年龄段的人玩的游戏,在游戏中可以进入数字的天堂,各种不同的关卡设计,还有千变万化的数字,都能让玩家燃烧自己的大脑,在这里可以选择四宫格的数字玩法,随着越来越熟练之后,可以挑战六宫格的数字计算玩法,在每一局当中都需要在规定的时间里完成挑战,可以随着时间的紧迫性,不断的超越自己的极限,在游戏中快速的转动大脑思维。
》》》》》#数独大全#《《《《《
2、《数字运算棋》
这款游戏中可以很好的锻炼玩家的计算能力,在游戏中可以挑战不同难度的关卡,而且每一个关卡当中的玩法都不同,玩家可以操作数字在这里变魔法,运用自己独到的计算能力,可以迅速解答出需要的答案,在这里可以获得极大的成就感,加减乘除任由玩家轻松的玩转,在游戏中可以锻炼自己成为数学小天才。
》》》》》#数字运算棋#《《《《《
3、《宝宝玩数字》

这是一款及其适合小孩子的数学思维游戏,可爱的动画场景可以吸引小朋友的注意力,而且还有教读数字的玩法,在这里可以从最基础的学起,还有可爱的小动物陪伴玩家,通过小朋友去数小母鸡下的蛋等,有趣的游戏互动玩法,可以激发小朋友的兴趣,还有游泳池等不同的主题场景,可以自由的进行切换,在快乐中可以学到很多的知识,在数学小农场当中开启快乐的夏天。
》》》》》#宝宝玩数字#《《《《《
4、《奥特曼学数学》

在这款游戏中给玩家打造了一个生动有趣的学习场景,在这里有小朋友们崇拜的英雄奥特曼,可以随时进行打怪兽,但是每一个关卡当中都要计算出一定得数学题,才可以击败小怪兽,而且还有多个不同难度的等级,在这里可以激发小朋友的胜负欲,快速的掌握计算的方法,营造一个快乐的学习环境。
》》》》》#奥特曼学数学#《《《《《
5、《超级数字》

在这里玩家可以进行轻松的闯关,在游戏中结合了消除和数字的玩法,让玩家能够在游戏中掌握数学知识,还能体会到数学的魅力,每一个关卡当中都有不同难度的数学题,只需要准确的解答成功,就会成功的进行消除,就可以在这里获得一个生命值,每一次答错就会扣除一个生命值,当玩家没有生命值的时候,则会闯关失败。
》》》》》#超级数字#《《《《《
上面这几款游戏就是今天小编分享给大家的2023数学游戏大闯关推荐,在这里玩家可以体验有趣的数学世界,而且还有很多精彩的小游戏,都能轻松的尝试,让玩家可以在数字王国里度过快乐的夏天。
野外生存实践好玩吗 野外生存实践玩法简介
期待已久的手游野外生存实践即将登陆九游,这款手机游戏吸引了大批玩家的关注,想下载这款游戏,有很多粉丝都在问九游小编野外生存实践好玩吗?野外生存实践值不值得玩?现在就为大家来简单分析下,看看这款游戏的玩法特点和游戏剧情介绍 。
野外生存实践快速预约/下载地址(需优先下载九游APP):
》》》》》#野外生存实践#《《《《《





1、野外生存实践简要评析:
非常棒的情况室逃生经验,激动的室逃脱类型的新游戏的游戏,很棒,这是一种新的 3D 房间逃脱游戏.为逃出房间或这种仿真环境,您需要的解决方案不同的任务.所以,你可以发现不同的对象合并这些项目成功逃出这里.分庭逃脱游戏,大的神秘问题惹你的脑,很有挑战性的神秘问题,游戏的目的是开着的门.得到自由,使用所有隐藏的对象来解决难题在会议厅,进入隔壁的房间里或下一个仿真环境.在这个充满乐趣,令人上瘾,自由和流行的益智游戏,挑战.操作非常简单,通过一系列操作,单击,幻灯片,g-传感器,为游戏.每个场景是一道难题,每个门是一个谜,线索留在现场通过游戏破解打开门,很多很难的益智游戏,不断更新.在这有趣,令人上瘾,自由和最受欢迎的益智游戏,挑战自己.行使的分析和推理技巧,你可以在你的电话上播放或平板电脑,无论在那里,你可以体验很有趣,如果你觉得这好笑,或你可以它分享给你的朋友,你可以侥幸吗?我们开始吧.
游戏特色: ↗ 心理训练!
↗ 流体运动!
↗ 智能手机拼图!
↗ 令人上瘾的小拼图!
↗ 华丽的图形和不同主题房间!
↗ 不断更新的新房间!
↗ 是免费的!
过来试试!
2、野外生存实践图片欣赏:





通过上面的游戏介绍和图片,可能大家对野外生存实践有大致的了解了,不过这么游戏要怎么样才能抢先体验到呢?不用担心,目前九游客户端已经开通了测试提醒了,通过在九游APP中搜索“野外生存实践”,点击右边的【订阅】或者是【开测提醒】,订阅游戏就不会错过最先的下载机会了咯!
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
梦幻模拟战青春的实践课 青春的实践课通关攻略
今天小编将会给梦幻模拟战的伙伴们带来青春的实践课通关攻略内容哟,还不知道具体打发的小伙伴们,都将可以把此次的游戏目光放入其中,以便可以让你轻松完成好此次的战斗挑战,赢下到丰富的游戏奖励哟,快快前往以下资讯内容掌握吧。

梦幻模拟战青春的实践课打法攻略
1、过关思路:波波放黑洞的时候,奶骑要提前用技能打BOSS上禁疗。波波放暗镰的时候,莉亚娜提前上个福音防晕。要小心黑洞和被动AOE的连招,很容易死人。假波波要尽快打死,不然BUFF叠多了很麻烦。
2、【花坦单挑思路】花T单挑BOSS,其他人躲开黑洞的范围,这样波波就不会放黑洞了,而且全程只招一次假波波。注意莉亚娜给花T上福音防晕,奶骑上被动回血,拉娜偶尔帮忙清一下小怪,其他时候都待机就行了。的随机点就是小怪,可以用时钟帮忙刷到拉娜可以秒的位置上,剩下的就可以抄作业了。
小编简评:
以上将会是小编此次所带来的梦幻模拟战青春的实践课通关攻略,还没有通关的小伙伴们,都将可以跟随小编的思路进行闯关,以便可以让你成功赢下到最终的比赛胜利。
ABC闪存卡为孩子好玩吗?怎么玩?ABC闪存卡为孩子游戏介绍
导读:期待已久的热门手游ABC闪存卡为孩子火爆来袭啦!这款手机游戏吸引了大批游戏玩家的的关注,有很多玩家都在问九游小编ABC闪存卡为孩子好玩吗?想知道这款手游怎么玩?今天九游小编就来说一下ABC闪存卡为孩子游戏介绍,带各位玩家详细了解一下这款手机游戏的所有玩法特点系统分析介绍,你就会知道ABC闪存卡为孩子究竟怎么玩,好不好玩了!
如果我们教与乐趣的孩子,他们会学到什么东西非常快而不单调乏味和捕获所有的东西非常快。 ABC闪存卡是一款非常不错的游戏为幼儿,教他们用不同的方式字母。不同的单词每个字母都会显示为动画图像和声音来。轻触单词图像按给定的指示,展现出惊人的动画。准备好学习与乐趣与这个惊人的教育孩子的游戏。关于GameivaGameIva为您带来最新创作或亲人大多数类别的游戏和应用程序,它们都非常受孩子们的喜爱。我们完全致力于建设与乐趣和学习更好的教育familiarities和享受为孩子们的人性化的游戏。留在我们在谷歌玩最新的更新或GameIva,并获得更多的还是益智游戏。到达我们:https://www.gameiva.com/跟随我们谷歌加:https://plus.google.com/u/1/103216636896495275888/posts像我们:https://www.facebook.com/GameivaGames跟随我们:https://twitter.com/gameivagames观看我们的比赛录像:https://www.youtube.com/channel/UCi8kgM_D4XgQPgYYA8BPnKA我们将与您的回复光滑。随时联系我们在wecare@gameiva.com任何问题和建议





看了上边的ABC闪存卡为孩子游戏介绍,各位玩家是否都了解了这款手游全部玩法特点系统分析介绍,知道ABC闪存卡为孩子怎么玩,好不好玩呢!快来九游下载玩游戏吧!
孩子们学习ABC闪存卡好玩吗?怎么玩?孩子们学习ABC闪存卡游戏介绍
导读:期待已久的热门手游孩子们学习ABC闪存卡火爆来袭啦!这款手机游戏吸引了大批游戏玩家的的关注,有很多玩家都在问九游小编孩子们学习ABC闪存卡好玩吗?想知道这款手游怎么玩?今天九游小编就来说一下孩子们学习ABC闪存卡游戏介绍,带各位玩家详细了解一下这款手机游戏的所有玩法特点系统分析介绍,你就会知道孩子们学习ABC闪存卡究竟怎么玩,好不好玩了!
学习单词的完全新的集合从AZ的所有字母。该动画奇怪的字符为每个对象,动物和鸟类的每个字母会帮助你理解的话更容易。从提高这些教育字母表游戏你的词汇和学习单词的所有字母和很多在同一时间。学习后,所有的话,你开始韵的学习活动,并带齐教育押韵,如字母童谣等等唱歌。





看了上边的孩子们学习ABC闪存卡游戏介绍,各位玩家是否都了解了这款手游全部玩法特点系统分析介绍,知道孩子们学习ABC闪存卡怎么玩,好不好玩呢!快来九游下载玩游戏吧!
3合1闪存卡好玩吗?3合1闪存卡游戏介绍
导读:期待已久的热门手游3合1闪存卡火爆来袭啦!这款手机游戏吸引了大批游戏玩家的的关注,有很多玩家都在问九游小编3合1闪存卡好玩吗?想知道这款手游怎么样?今天小编就来说一下3合1闪存卡游戏介绍,带各位玩家详细了解一下这款手机游戏的所有玩法特点系统分析介绍,你就会知道3合1闪存卡究竟怎么样,好不好玩了!
3合1闪存卡是一个为幼儿的学习工具。这个应用程序是非常容易使用。你的孩子可以选择学习ABC,数字1到10和形状。


看了上边的3合1闪存卡游戏介绍,各位玩家是否都了解了这款手游全部玩法特点系统分析介绍,知道3合1闪存卡怎么样,好不好玩呢!
相关专题
最新专题
- 我不是mt中文版下载
- 快车道中文版下载
- 狼牙刃中文版下载
- 魔幻立方体中文版下载
- 忍者斗恶龙中文版下载
- 灵之秘境中文版下载
- 火柴人勇士对决中文版下载
- 守塔英雄中文版下载
- 宝宝数数中文版下载
- 月亮阴影中文版下载
- 控制塔中文版下载
- 樱花小镇假期生活中文版下载
- 公主城堡房间中文版下载
- 宝宝飞行员中文版下载
- 雪球大冒险中文版下载
- 简单世界中文版下载
- 莱特鸡中文版下载
- 洪荒之剑中文版下载
- 点球大师中文版下载
- 蓝图中文版下载
- 绝地求生大逃亡中文版下载
- 懒惰中文版下载
- 嗜血大陆中文版下载
- 哈喽世界中文版下载
- 梦幻爱拼图中文版下载
- 火车司机驾驶模拟器中文版下载
- 僵尸高中中文版下载
- 雷霆之刃中文版下载
- 捞金鱼中文版下载
- 快速型中文版下载
游戏排行
即将上线










最新游戏
最新资讯


















































 粤公网安备44010602000283号
粤公网安备44010602000283号
