数学迷阵游戏介绍
数学迷阵简介
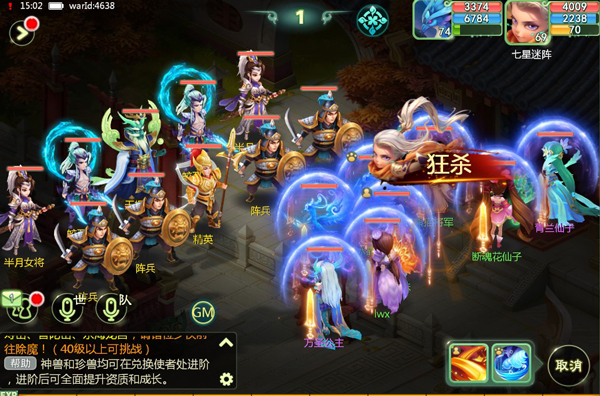
数学迷阵游戏截图






大家都在看-热门推荐
太极迷阵规律是什么 通用数学规律推荐
在太极迷阵里,即使是再难的智力游戏,也是包含一定数学规律的,就是看能不能发现。相信很多玩家都卡关了,因此掌握规律规律非常有助于大家顺利通关,下文就为各位带来具体规律的介绍,一起来看看吧!
规律攻略
在这里给出n个点,m条线,任意线条件约束(例如线连的点必须连续),任意初始点a,任意终止点b的通解思路。
黑白二色对应二进制0和1,则n个点对应于二进制向量,线约束对应于n*n的二进制矩阵A,则本问题转化为解二进制线性方程组A*x=a+b。
从而有,有解的充要条件是r(A)=r([A a+b]),这里的秩是指字母矩阵(λ-矩阵)的秩,不是数字矩阵的秩。
因此,我们只需要1次秩的判断就可以解出该问题。
该解法总计算量约为(m-1)(n-1)/2,实际计算更简单,因为只涉及到0和1的二进制加减。
若用计算机判断秩,我们可以选用n-1次秩的判断代替手工计算,虽然计算量增大,但总计算量不过是大约为m*O(n2),甚至更少。
实际上,只需要一次对角化,就可得出结果,因为只涉及到二进制加减,总计算过程运算量极小。
给出例子:以第五关为例(高阶类似)

共6个点,4条相连的线,初始点a=(1,0,0,0,1,0),终止点b1=0或b2=(1,1,1,1,1,1)
矩阵A如下图(左边灰色是行标):

得出结果:
若取b=b1,有x=(1,1,1,0,0,1),(选取初始列不同,得到结果不同,但本解是包含所选列的极小解)
若取b=b2,则无解
以上就是太极迷阵规律是什么的全部内容,不知道各位亲爱的小伙伴是否掌握了呢?希望能提供些帮助!如果还有其他疑问,欢迎访问本站的相关文章。
揭秘以太极迷阵背后的数学规律 探究以太极迷阵的数学奥秘
不仅趣味性十足,而且在游戏过程中充满了许多数学问题,以太极迷阵是一款历史悠久的游戏。球的移动和等等、这些问题包括不同颜色球的排列组合。帮助大家更好地理解这款游戏、本文将会为大家深入探究以太极迷阵背后的数学规律。

以太极迷阵的基本规则
玩家需要用鼠标将球放置到正确的位置上、以太极迷阵是一款非常经典的游戏。玩家需要注意球的颜色和位置、不同颜色的球需要放置到相应的位置上,在游戏过程中。
以太极迷阵中的数学问题
但是却充满了许多数学问题、以太极迷阵看似简单。球的移动问题,球的问题等等,其中包括了排列组合问题。

球的移动规律
球的移动是一个非常重要的问题,在以太极迷阵中。玩家需要考虑如何让球移动到正确的位置上。这也是一个数学问题、在这个过程中,玩家需要理解球的移动规律。
问题
问题在以太极迷阵中也是非常常见的。这个问题主要是涉及到球的颜色和位置的关系。玩家需要根据不同颜色的球和不同位置的球进行操作。
排列组合问题
排列组合问题也是以太极迷阵中的一个难点。这个问题主要是涉及到不同颜色球的排列组合问题。才能够完成游戏、玩家需要考虑每一个颜色球的排列组合问题。

数学规律应用实例
下面举个实例来说明数学规律在以太极迷阵中的应用。分别是红,在某一关卡中,绿、黄,蓝四种颜色,有四个不同颜色的球。这些球需要放置到相应的位置上,放置规则如下:绿球放置在C位置,黄球放置在B位置,红球放置在A位置,蓝球放置在D位置。
基本数学公式
我们需要掌握一些基本的数学公式、在解决以太极迷阵中的数学问题时。公式,球的移动公式等等、这些公式包括排列组合公式。
排列组合问题的解法
排列组合问题是以太极迷阵中最为常见的问题之一。并且根据游戏情况进行灵活运用,解决这个问题需要掌握排列组合公式。
问题的解法
问题是以太极迷阵中比较难解决的问题之一。找到正确的放置位置、解决这个问题需要考虑不同颜色球之间的关系。
球的移动问题的解法
球的移动问题在以太极迷阵中也是一个重要的问题。找到解决方案、解决这个问题需要考虑球移动的轨迹和球的数量。
数学规律的应用场景
数学规律的应用场景在以太极迷阵中非常广泛。、可以帮助玩家更快地完成游戏、球的移动等多个方面、这些规律包括了排列组合。
数学规律的优点
数学规律在以太极迷阵中有很多优点。它可以帮助玩家更快地完成游戏;它可以提高玩家的数学能力和思维能力。
数学规律的局限性
但是它也有一定的局限性,虽然数学规律在以太极迷阵中非常有用。数学规律可能并不能完全解决问题、在一些特殊情况下。
数学规律的应用前景
未来随着游戏玩法的不断变化和发展,数学规律在以太极迷阵中应用前景非常广泛、数学规律也将变得越来越重要。
以太极迷阵是一款非常有趣并且具有数学问题的游戏。问题和球的移动问题等多个方面的数学规律、在游戏过程中、玩家需要掌握不同颜色球的排列组合问题。提高数学能力和思维能力、掌握这些规律可以帮助玩家更好地完成游戏。
探寻以太极迷阵规律的数学奥秘 玩转以太极迷阵 揭开通用数学规律
玩法多样的游戏,以太极迷阵是一款趣味性十足。要想取得胜利、在这个游戏中,还需要掌握一些数学规律,不仅需要灵活的思维和敏捷的反应能力。并为大家呈现出一份详实而有趣的攻略,本文将重点探讨以太极迷阵中的通用数学规律。

一、以太极迷阵中的基本操作
旋转,以太极迷阵中的基本操作包括移动,对称等。旋转则是指将整个棋盘按照某个中心点旋转一定角度、移动是指将棋子从一个位置移到另一个位置,对称则是指将整个棋盘按照某个轴线进行对称。
二、以太极迷阵的基本规则
不能踩到对方的空位、不能堵死对方的棋子等,以太极迷阵的基本规则包括棋子不能跨越对方棋子。如不能将一个棋子对称到另一个棋子的位置等,对称操作还有一些特殊的规则。

三、以太极迷阵中的常见策略
保持灵活性,在以太极迷阵中、常见的策略包括攻守兼备,争取先手等。积极寻找进攻机会,攻守兼备是指在保护自己棋子的同时;保持灵活性则是指避免让自己的棋子陷入死角;占据先机,争取先手则是指尽可能让自己的棋子先行动起来。
四、以太极迷阵中的数学规律之对称
对称是以太极迷阵中最为重要的数学规律之一。而轴线的位置和方向则会对游戏产生巨大影响、在对称操作中,所有的棋子都会围绕着某个轴线进行对称。只需要放置两个棋子就可以直接获胜,比如,在一个以左上右下对称为轴线的局面中。
五、以太极迷阵中的数学规律之旋转
旋转也是以太极迷阵中的重要数学规律之一。而旋转的角度则会对游戏产生巨大影响,整个棋盘都会以某个中心点为轴心进行旋转、在旋转操作中。在一个以棋盘中心为轴心旋转60度的局面中,比如,只需要放置两个棋子就可以直接获胜。

六、以太极迷阵中的数学规律之平移
平移是以太极迷阵中最为基础的数学规律之一。而平移的距离和方向则会对游戏产生影响,在平移操作中,所有的棋子都会沿着某个方向进行平移。在一个以水平方向进行平移的局面中,比如,可以通过放置两个棋子来控制整个局面。
七、以太极迷阵中的数学规律之组合
对称、它们相互组合可以产生更加复杂和多样化的游戏局面、旋转和平移都是以太极迷阵中的数学规律。在一个同时进行对称和旋转操作的局面中、只需要放置一个棋子就可以直接获胜、比如。
八、以太极迷阵中的数学规律之对角线
对角线也是以太极迷阵中的一种重要数学规律。只需要放置一个棋子就可以直接获胜,在一个以对角线为轴线进行对称的局面中。也存在类似的获胜策略,在以对角线为轴心旋转90度的局面中。
九、以太极迷阵中的数学规律之奇偶性
奇偶性是以太极迷阵中的一种基础数学规律。只需要放置一个棋子就可以直接获胜、在一个以奇数行,偶数列进行对称的局面中。
十、以太极迷阵中的数学规律之对称性
对称性是以太极迷阵中的一种重要数学规律。只需要放置一个棋子就可以直接获胜,在一个以对称性为特征的局面中。对称点的位置也会对游戏产生影响,在进行对称操作时。
十一、以太极迷阵中的数学规律之对手策略
我们不仅需要掌握自己的策略,在以太极迷阵中,还要研究对手的策略。我们可以利用对称或平移操作来掌控局面,比如、在对手进行旋转操作后。
十二、以太极迷阵中的数学规律之胜利策略
胜利并不总是通过获得更多的棋子来实现的、在以太极迷阵中。只需要放置一个棋子就可以直接获胜,有些局面中。不断寻找胜利的机会、在游戏中、我们要时刻保持敏锐的观察力和灵活的思维能力。
十三、以太极迷阵中的数学规律之劣势策略
有时候我们会处于劣势局面,在以太极迷阵中。制造混乱等,此时,挑战对手、我们需要采取一些特殊的策略、如妨碍对手。
十四、以太极迷阵中的数学规律之平衡策略
平衡策略是非常重要的,在以太极迷阵中。并尽可能保持局面的平衡,在游戏中,我们需要保持自己的棋子和对手的棋子数量相当。增加自己的防守能力、这样可以减少对手的攻击机会。
十五、
其中蕴含的数学规律也是不可忽视的、以太极迷阵作为一款趣味性十足的游戏。旋转、保持灵活性,对角线,掌握对称、平移等基础规律,对称性等深层次规律,才能够在游戏中获得胜利、研究奇偶性,在游戏中,争取先手等策略,以及灵活运用攻守兼备。
声音迷阵好玩吗 声音迷阵简介
如果人们要对自己生活中发生的事有更多的发言权,获得更多开发自己能力的自由,就必须帮助人们获得那些已知存在、但并不拥有的知识。我的意思不是说给每人一台电脑让他们自求多福,这又从哪里开始呢? 我是说,试图找到翻译知识的方法,教我们提出正确的问题。
我们正处于通信技术革命的边缘,这使翻译知识比以往任何时候都更有可能;但如果不这样做,将导致知识的爆炸。使我们之中没有接触到它的人,像聋哑,失明一样无能为力。我认为大多数人都不希望这样。
那我们应该怎么办?我不知道,但也许一个好的开始,是认识到自己有理解任何事情的能力,因为这种能力是存在的,只要事物被解释得足够清楚。之后,去寻求解答。
----JAMES BURKE

wasd控制前后左右,左shift改变速度,空格键跳跃,鼠标左键点击与物品互动。
如果迷失方向,建议玩家闭上眼睛。

《和平精英》机巧迷阵攻略 机巧迷阵通关技巧分享
和平精英机巧迷阵怎么通关?有些小伙伴还不是很清楚,机巧迷阵是游戏最新模式奇幻之旅的地宫特殊玩法之一,那么这个机巧迷阵有没有什么通关技巧,接下来就和小编一起来了解下通关攻略。
和平精英机巧迷阵通关攻略
1、地宫刷新位置

2、关卡1——棱镜反射
在棱镜反射关卡内,存在固定位置的多个棱镜,需要对棱镜的朝向角度进行调整。
当入口处的光线,通过棱镜折射后成功射向出口的大门时,大门开启,可以进入下一个关卡!
注意:其中有两个棱镜是自转的哦!

这个关卡特别考验大家的动手能力以及团队协作能力,建议跟队友一起来闯关。
3、关卡2——记忆方块
记忆方块关卡,从入口到终点有4*4的方块阵型,但每一行只有1个方块是正确的,只有一直踩到正确的方块才能抵达终点。
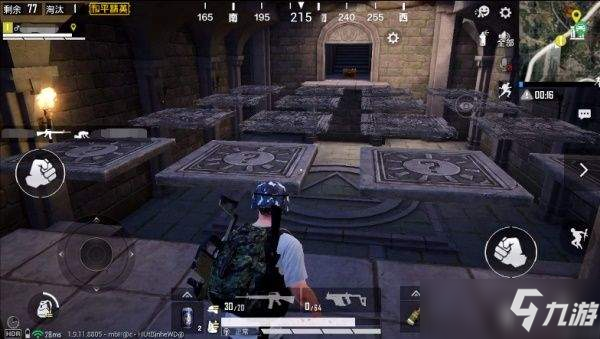
踩到错误的方块会踏空,需要重新进行挑战,可以放心的是,方块的正确位置单局内并不会发生变化!

这个关卡考验的是大家的运气及记忆力,只有通过了这个关卡,才能拿到最终的宝箱奖励!
闯过地宫的所有关卡之后,可以获得一个堪比空投箱高级资源的宝箱奖励!
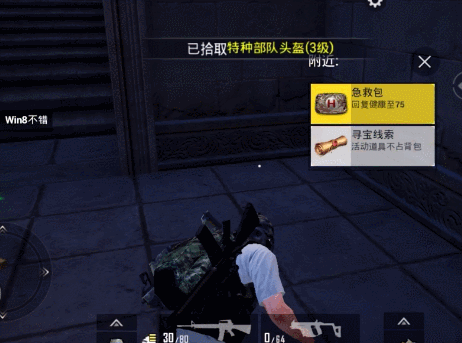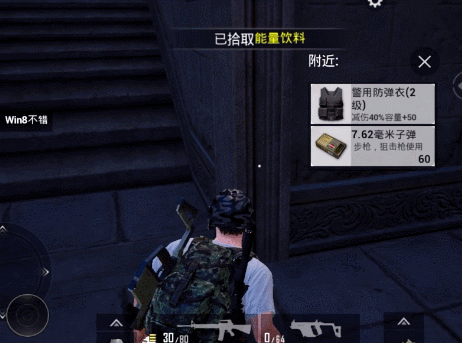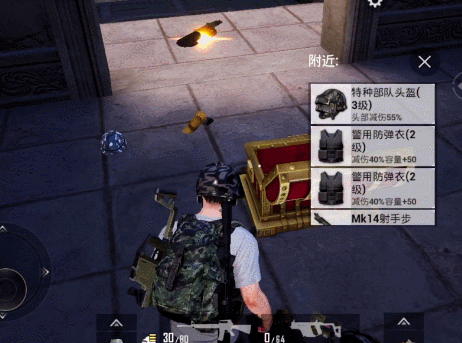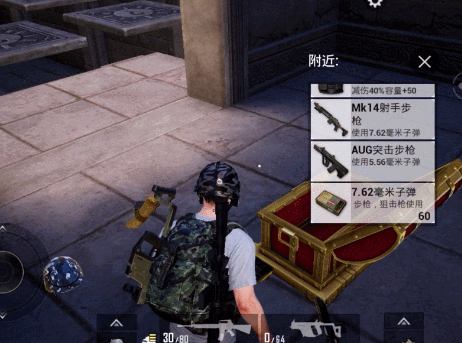
以上就是和平精英机巧迷阵通关攻略的全部内容了,希望能对大家有所帮助。
拳皇命运黑晶迷阵怎么玩 黑晶迷阵玩法技巧
拳皇命运黑晶迷阵怎么玩?黑晶迷阵是游戏中3V3多人竞技玩法,作为一个强调配合的组队活动,究竟该怎么玩呢?下面小编就带大家一起去看一下拳皇命运黑晶迷阵玩法攻略!

黑晶迷阵
1、黑晶迷阵分为蓝方和红方两个队伍,每个队伍共有3名玩家。
2、双方各拥有两座黑晶防御装置和一座主基地,摧毁对方主基地获得胜利。

3、主基地和第二个黑晶防御装置自带防护罩,抵挡一定伤害,5秒未受到攻击将自动修复,击毁前一个建筑后护罩会消失。
4、双方的第一个黑晶防御装置存在时将定时生产出恢复药水。
数学游戏 我爱数学
「我爱数学:MathMathMath」是一款寓教于乐的数学类游戏,画风比较学院,非常适合小朋友玩,在玩游戏的过程中不知不觉学习数学知识,我爱数学,数学使我快乐~
九游括三种模式:
多人游戏:在同一个iPad或者手机上尽快点击正确的答案并收集积分,第一个拿到10分的赢得比赛。
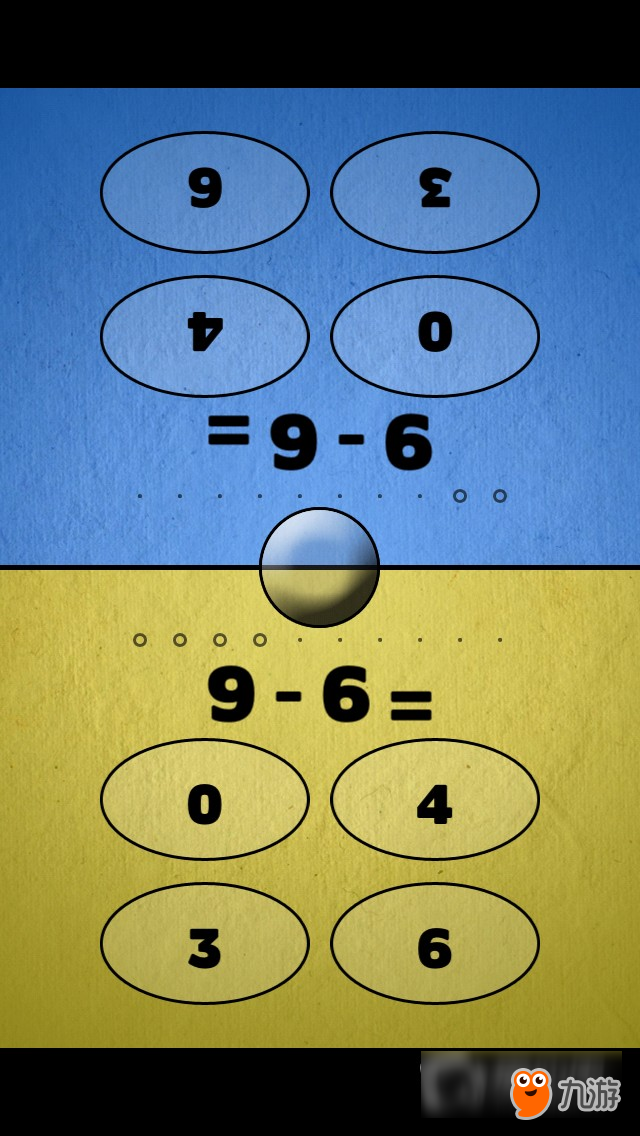
青蛙游戏(单人游戏):点击正确的答案则青蛙就能吃到食物,否则就会失败。
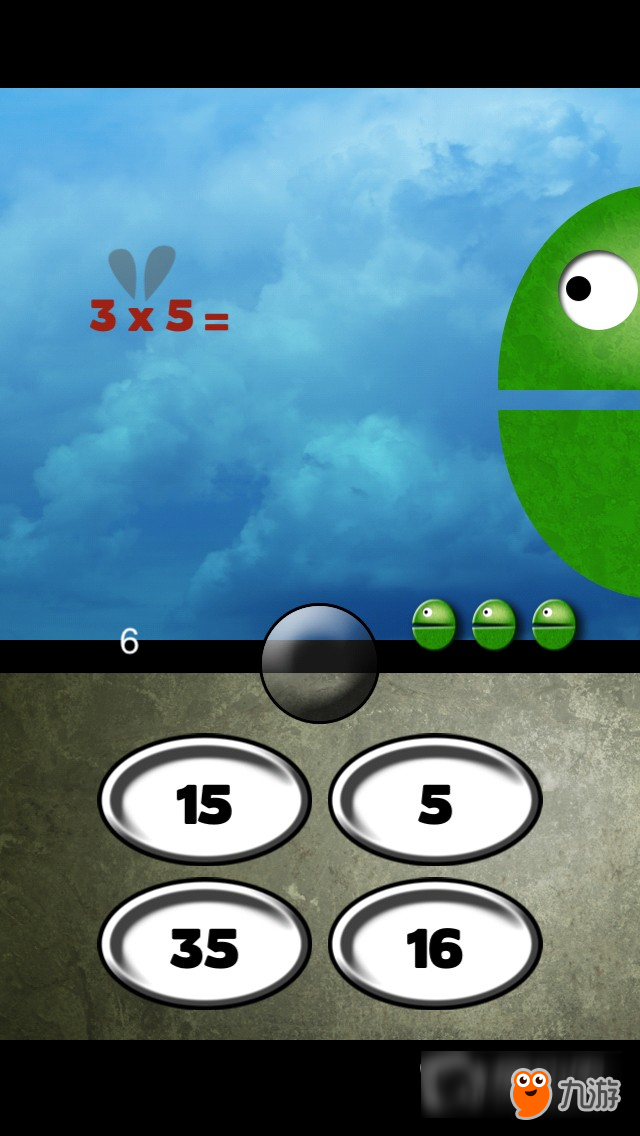
相机游戏(单人游戏):- 同时改善你的健身和你的精神数学技能!游戏可以直接从相机图像中检测出你的动作!在相机前移动,并在空中触摸正确的答案。使用iPad智能外盖将iPad放在直立位置,然后在相机前方跳动,或将设备平放在桌子上,并将其中一根手指移动到相机前方。注意:仅适用于具有正面(面对面)相机的设备(iPad第2代和更新版,iPod第4代及更高版本)。

难得一见的寓教于乐的数学游戏,赶紧下载起来吧~

七星迷阵
独乐乐不如众乐乐,小伙伴的力量是无穷的,更何况悟空再强,关键时刻也需要请救兵,想突破迷阵、快速闯关?拉上小伙伴一起行动吧。
每周三晚上 20:00-20:40,玩家等级达到40级,即可在凌霄宝殿 与 玉皇大帝 进行对话,开启多人组队PVE副本“七星迷阵”。 组队规模为3-5人,不足5人可上伙伴。

图1
打败场景内小怪,可获得强力buff,打败守关怪物,可跳到下一关,除了正常奖励还会有有翻牌奖励,打败7个守关boss,即通关副本。
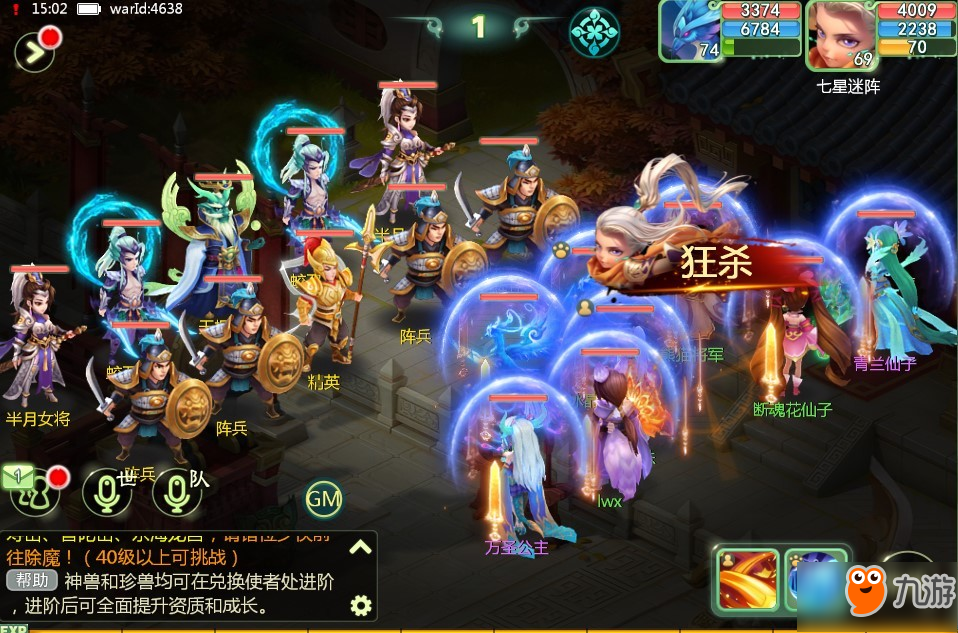
图2
前10队通关的玩家可以获得额外的奖励。
在活动地图内,变更了队伍内成员,会变得无法记录通关时间,并且不会获得通关奖励。
如转载涉及版权等问题,请作者与我司联系,我司将在第一时间删除或支付稿酬。
相关专题
最新专题
- 2022好玩的奥特曼小游戏
- 有哪些有关数字的游戏盘点
- 2022人气最高的卡牌rpg手游排行榜
- 2022有趣的萌宠游戏排行榜
- 2022大型解谜类游戏排行榜推荐
- 2022好玩的像素游戏下载大全
- 2022高人气建筑的游戏
- 2022主角是机器人的游戏有哪些
- 下载最多的游戏排行榜推荐2022
- 2022即时战斗手游排行榜前五
- 三国卡牌养成类手游推荐2022
- 2022年流行的热门网络手游有哪些
- 2022最近很火的修仙游戏叫什么名字
- 简单游戏有什么好推荐的2022
- 2022值得推荐的经典解谜游戏
- 2022类似街头霸王闯关的游戏叫什么
- 2022低配置单机游戏排行榜
- 2022年有趣的大冒险的游戏有哪些
- 2022受欢迎的挂机修仙手游排行榜
- 宫廷选择命运的游戏有哪些2022
- 2022海贼王最新手游有哪些
- 2022手机闯关游戏排行榜大全
- 2022十大画质唯美古风手游下载
- 2022好玩的三国手游推荐大全
- 2022吃鸡游戏下载大全推荐
- 2022单机狙击游戏排行榜前十名
- 2022什么游戏火有哪些
- 2022年最良心的三国卡牌游戏榜单
- 好玩的三国志系列游戏大全推荐2022
- 2022类似逃离塔科夫类型游戏
游戏排行


即将上线









最新游戏
最新资讯


















































 粤公网安备44010602000283号
粤公网安备44010602000283号
