火柴数学题

在星露谷物语中，玛鲁是可以结婚的女性npc之一，她喜欢搞小发明，有时候玛鲁会提出些问题，其中有人问星露谷物语玛鲁数学题怎么过？下面一起来看看星露谷物语玛鲁数学题答案解析吧。

星露谷物语玛鲁数学题答案是什么

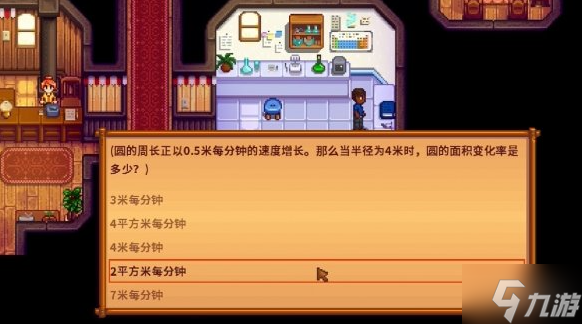
问：圆的周长正以0.5米每分钟的速度增长。那么当半径为4米时，圆的面积变化率是多少？

答：2平方米每分钟

1、3米每分钟

3、4平方米每分钟

3、4米每分钟

4、2平方米每分钟

5、7米每分钟

答案解析：

1、圆的周长与半径之间的关联可表示为：[ C = 2pi r ]设想圆的周长以每分钟0.5米的速率递增，即：[ frac{dC}{dt} = 0.5 text{ m/min} ]本研究旨在确定半径为4米时，圆的面积变化速率。

2、面积 ( A ) 与半径 ( r ) 之间的数学关系为：[ A = pi r^2 ]首先，我们需计算出面积的变化率 ( frac{dA}{dt} )。

3、利用链式法则，可得：[ frac{dA}{dt} = frac{dA}{dr} cdot frac{dr}{dt} ]由于 ( A = pi r^2 )，对 ( r ) 求导得：[ frac{dA}{dr} = 2pi r ]接着，我们需要确定 ( frac{dr}{dt} )。

4、由 ( C = 2pi r ) 对时间 ( t ) 求导，得：[ frac{dC}{dt} = 2pi frac{dr}{dt} ]将 ( frac{dC}{dt} = 0.5 ) 代入上式，解得：[ frac{dr}{dt} = frac{0.5}{2pi} = frac{1}{4pi} text{ m/min} ]

5、目前，我们有：[ frac{dA}{dt} = 2pi r cdot frac{1}{4pi} = frac{r}{2} ]当 ( r = 4 ) 米时，计算得到：[ frac{dA}{dt} = frac{4}{2} = 2 text{ m}^2/text{min} ]

6、所以，当半径为4米时，圆的面积以每分钟2平方米的速率变化。综上所述，圆的面积在半径为4米时，其变化率为2平方米每分钟。

为大家推荐：星露谷物语玛鲁的行程是什么-玛鲁所有行程查看方法

关于星露谷物语玛鲁数学题答案分享小编今天就为大家讲解到这里，希望大家能够喜欢，更多的精彩游戏资讯请关注九游下载站，这里有最新的热门游戏资讯。

数学也确实很烧脑，现在有很多的游戏中也掺杂了一些数学的因素，比如火柴数学题游戏也就成为大枷锁，关注的近一段时间有很多小伙伴也会问一问，到底哪一款火柴数学题游戏更好玩呢？小编也给大家分享几款不错的游戏，不仅仅能够开拓你的思维，还能带来更好的乐趣，下面一起来认识一下。

1、《解密火柴谜题》

《解密火柴谜题》是很休闲、益智类型的游戏。也是属于火柴游戏的一种，有诸多不一样的关卡游戏，不仅仅很精致，还能锻炼你的脑力。各个年龄段的玩家都适合，在开拓自己动脑能力的过程中还可以通过简单移动火柴棍的方式去解开谜题，是不是很有乐趣呢？如果你也想要找寻这种类型的游戏，这款就值得你挑战的呢。好玩的火柴数学题游戏，小编只找到以上一款，还有其他火柴的游戏也值得你去玩耍，来看一看。

》》》》》#解密火柴谜题#《《《《《

火柴数学题游戏只找到上面一款，给大家介绍几款其他的火柴类型游戏！

2、《火柴人战争》

你也想要去找到一款刺激类型的游戏吗？那么《火柴人战争》也是值得去挑战。玩家在一个叫做nota的世界当中，作为统领在统治着国家，当然每个国家的人都有自己的防御能力、攻击的能力，它们都是觉得自己的武器比较高超，在游戏当中你带领的火柴人士兵不断的去攻击、打退敌人之后才能意味着胜利，快带领着你的火柴人赶快行动吧。

》》》》》#火柴人战争#《《《《《

3、《火柴人奇袭》

《火柴人奇袭》游戏不仅仅有着精致的画面，也是属于一款跑酷类型的游戏，玩家需要通过跨过一道一道的障碍之后，才能躲避迎来的陷阱。当然到达终点之后你就获取了成功，这款游戏的关卡确实比较多，也是休闲类型的游戏，能给你带来更多的乐趣。想要体会一把火柴人游戏所带来的快感吗？那么这款游戏值得你去挑战，赶快来行动吧。

》》》》》#火柴人奇袭#《《《《《

4、《火柴人足球》

现实中有很多的小伙伴也是喜欢踢足球的，那么《火柴人足球》是模拟踢足球的游戏，游戏的玩法也很简单，当然游戏的界面也是很简单明了的操作的模式也并不很困难，通过控制屏幕上的虚拟遥控控制方向，这样才能够去传球接球在进攻和防守抢断的过程中，也有着更多的比赛模式，是很有趣的一款游戏呢。

》》》》》#火柴人足球#《《《《《

5、《火柴人觉醒》

《火柴人足球》游戏具备着很好的冒险性，不仅仅能够带来更加精致刺激的画面，在游戏中玩家当做一名火柴人，触碰屏幕的火柴人进行移动、跳跃或、攻击等多种动作，当然只有穿越各种关卡之后才有着不一样的设计、难度。总体来说，这款游戏确实很让人上瘾，画面感也特别精致，能带来更多的乐趣，赶快尝试吧。

》》》》》#火柴人觉醒#《《《《《

2024好玩的火柴数学题游戏有哪些？已经做了详细的介绍，画面感、玩法都很不错，值得体验。你也喜欢火柴人的游戏就可以选择上面的几款，真是不错的乐趣呢，赶快点击下载的按钮吧！

可口的披萨美味的披萨小男孩数学题怎么过?很多小伙伴不清楚小男孩数学题怎么做好？今天小编就给大家带来可口的披萨美味的披萨小男孩数学题通关攻略，希望可以帮助到有需要的玩家。

可口的披萨美味的披萨小男孩数学题通关攻略

配方：

两个披萨：一个用白面饼，一个用全麦面饼，两个面饼都加酱料芝士和一半猪肉粒

以上是小编为各位带来可口的披萨美味的披萨小男孩数学题通关攻略的全部内容，更多精彩游戏资讯，请持续关注九游。

在幻书启世录手游中艾斯数学题究竟该怎么做呢？题目答案内容又是什么样的呢？不清楚的话，接下来就让我们一起来看一下吧~！

幻书启世录手游艾斯数学题答案详解

刚刚在刷数学本，然后突然艾斯跳出来问了一道排列组合数学题

题目大意 ...

要攻略魔神王和阎罗王，但是每位前面都有编号为1-4的4个幻书挡路，打了编号小的才能打编号大的，问一共有多少种攻打方式

答案 ...

252，插空法的话比较好解

第二题 ...

斐波那契数列的经典内容，不描述了，55(明明是110只羊)

第三题 ...

叶初始有100暴击率和150暴击伤害，她可以降低自己x暴击率提升x暴击伤害，问x为多少时伤害期望最高。这是二次函数最值题，配方算一下就知道应该是25%

第四题 ...

罗宾和夏洛蒂从4个委托里各随机选两个，问两人恰好有一个任务相同的概率是多少。 答案是1/3，比较基础的组合概率题

初恋日记中有着上学的剧情，比较重要的就是考试了，其中数学题带有一定的专业性，很家不会做，初恋日记数学答案怎么查看，A=1-1/2+1/3-1/4+...+1/99-1/100，B=1/(101²-1²)+1/(102²-2²)+...+1/(150²-50²)，那么A/B的值是多少。

数学题答案一览

1.已知：A=1-1/2+1/3-1/4+...+1/99-1/100，B=1/(101²-1²)+1/(102²-2²)+...+1/(150²-50²)，那么A/B的值是多少?

(B)

化简过程省略

A.100 B.200 C.300 D.400

2.已知正数a，b，c满足：5c-3a≤b≤4c-a，clnb≥a+clnc，则b/a的最大值是( )。

(A)

解析过程省略

A.(0.5,3.5) B(0.8,2.3) C(1,3) 3.5/0.5=7 最大值为7

3.3.已知A(2,3)，原点(0,0)，B是平面内的一点，△AOB为直角三角形且OB=2，试求满足条件的B点坐标( )。

首先需要确定的是，平面内满足上述条件的B点共几个?

(D)

A、1个 B、2个

C、3个 D、4个