神匣庆典活动抽奖技巧 钥匙如何使用最优化

✦结论✦

小层留下条件

剩12个或12个以下格子还有两个奖励

剩7个或7个以下格子还有一个奖励

大层无脑奖励全拿

小层开一个就走的每层期望次数：9.25

小层在上述操作下的每层期望次数：≤9.654295

大层开三个走的期望次数：27.75

小层开一个就走大层开三个走，整10层期望次数：111

小层附加条件大层开三个走，整10层期望次数：≤114.638656

小层的停留也要考虑剩余钥匙量

要保证整10层有足够钥匙量获取奖励。10层还是大头，权重很高

✦推导过程✦

【第一步】

计算拿一过、拿三过钥匙期望。

通过超几何分布，使用EXCEL，构建万能公式计算器。计算拿一过、拿三过钥匙期望。

(我也没看懂)

【第二步】

以“小层尽量快过，大层奖励拿满”为基础，推到出钥匙平均价值

(思路鸣谢libin大佬)

第二步折算幺九层、整十层三个奖励的平均钻石期望，再结合幺九层首拿速过，整十层三个拿满的基本方针，通过第一步计算出的钥匙期望，算出一轮十层过完的总钥匙数期望和总钻石收益期望，做商求出一整个周期内的钥匙对应价值(后面我们称之为钥匙平均价值)。

【第三步】

逐个计算不同情况时剩余格子的价值期望，高于钥匙平均价值则留下，否则反之

(思路鸣谢光饼二佬)

第三步使用万能公式计算器，逐个计算剩余格子、剩余奖励对应情况下的，本层钥匙对应价值，并将其与钥匙平均价值作出对比，如果高于平均价值则留，低于平均价值则走。

【第四步】

第四步沉声计算，完善细节。

【花絮】

·第一遍单奖励次数期望算错了。。

·偶然发现次数期望公式，可以处理源算法超几何分布无法解决的分数格子的问题

·期望下的获得奖励不会改变该层钥匙对应钻石期望

·该层要获取奖励的数量在初始条件下不会改变该层钥匙对应钻石期望

·细节：小层附加条件下，会额外增加钥匙的消耗量，也会额外增加钥匙的平均价值，但是在加权平均中权重过低(经计算权重<1%)，而计算过于复杂，舍掉了，钥匙平均价值确定为预计算值

·细节：小层附加条件下，对白嫖玩家开满30层奖励的影响略小，所以需要额外注意的操作手法舍掉了，但是预留了各个层数各个环节的钥匙使用期望，供读者自行拿捏，翻车别喷我家娇娇

然后万能公式大概是。。长这个样子。。(平均价值计算页在另页，篇幅很小，也很简单，就不附了)

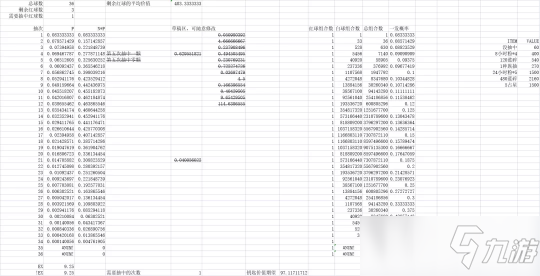
物品的价值按的是我的偏好来计算的，结论应该出入不大