围住神经猫攻略 数学大神教你成功围住神经猫

“围住神经猫”虽然是一个小游戏,但细细想来,其实也是一个很有意思、值得探讨的数学问题。
先抛出结论:
在原游戏的条件下,由于初始占有点的随机性,在考虑最坏情况下(如一个点都没占有),无法确保围住神经猫。但是,当棋盘扩展到一定程度时(M不小于9,M的定义会在下面说明),无论初始状态如何,存在策略,必能围住神经猫。
下面给出本人对这个问题较为详尽的分析,个人观点,仅供参考。
从表面上看,神经猫能走到的格子数是 9×9=81 格,但这个“棋盘”并不是对称的,神经猫只需要走 4 步就能到棋盘的边缘,而一旦被神经猫逃到棋盘边缘,游戏就结束了。
神经猫的逃跑策略是贪心算法,也就是说,它总是考虑当下离边缘最近的路线。
实际上,如下图所示,神经猫 4 步可以走到的格子被深红色标出,其中带五角星的是棋盘的边缘。

浏览原图
神经猫显然会尽可能地往带五角星的格子逃跑,而我们要做的便是在猫到达五角星格子以前,把它拦住。
为了便于讨论,我们考虑更具有代表性的问题,如下图所示:
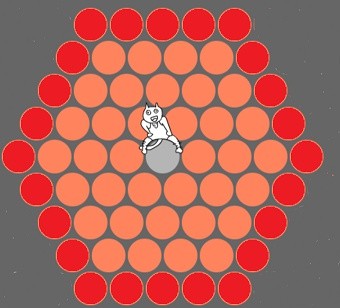
浏览原图
问题描述:在一个边长为 M(上图中 M=5)正六边形的棋盘上,要在最坏情况下,依然确保能抓住神经猫,令最小能满足条件的 M 为 N,求 N 的值。
下面证明,N=9。
如觉得证明过于数学化,可跳过该证明,直接看文末总结的本游戏技巧。
———证明开始的分界线———
你真的想看证明过程吗?
数学控请点击“”查看。
———证明结束的分界线———
回到原游戏。从上面的分析可以感受到“围住神经猫”的技巧精髓有如下几点:
0、游戏的精髓,不是用最少的步数围住神经猫,因为就步数而言,受开局影响太大,主要靠运气;游戏的精髓,是在特定开局情况下(我无法改变):
(1)尽最大可能,确保围住神经猫;
(2)在确保(1)的情况下,尽可能使包围圈小,从而减少围住它的步数。
1、慎勿轻速。除非有援兵,否则应该要远远地张开一张大网,在己方很弱的情况下,切勿轻敌。因为你的速度不比神经猫快,所以直接近身堵截,你总是会慢一步。当你在部署完防御之前,和神经猫短兵相接,你就跪了。
2、包围圈的设计。
由引理 3,有推论:当神经猫和我的包围圈短兵相接之前,如果神经猫足够聪明,我必须保证,在我的包围圈,已经布置至少 7 个子。且尽可能在 6 个方向上都有子力分布。
如下图所示,如何围住神经猫?
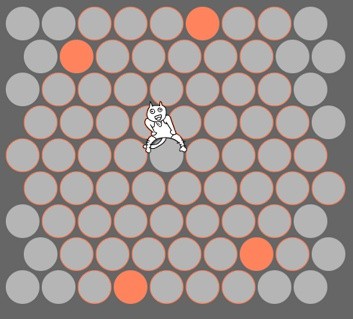
浏览原图
易见,神经猫至多 3 步就可以与我的防守子力短兵相接。而我设计的包围圈已经有了 4 个子,所以我接下来的 3 个子,都必须用于包围圈的设计。
如下的包围圈是可行的:
浏览原图
然后就开始撒下大网:
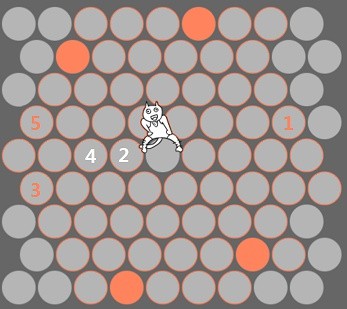
浏览原图
至红 5,大网所需的 7 点已经占领完毕,神经猫已经无法逃出。
如果它负隅顽抗,参见下图,至 40,它终于进入了包围圈。
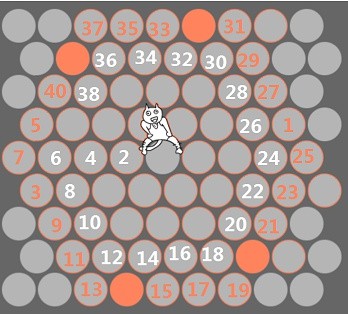
浏览原图
但是如果包围圈设计得不好呢?如下图所示,左下角的包围圈,神经猫只要 2 步就可以短兵相接了。
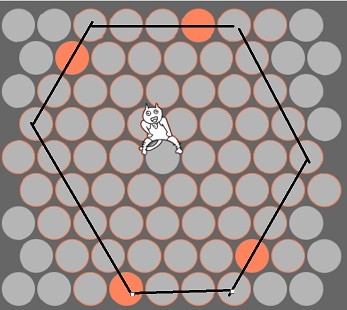
浏览原图
如下图,到白 4,实际上你已经围不住神经猫了。
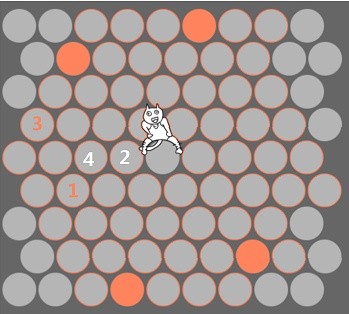
浏览原图
接下来的攻防如几乎是必然的,至白 26,神经猫安然逃出。

浏览原图
所以,设计包围圈是很重要的!能不能围住就在可能就在 1 步之间!
(注:本例证明了,如果神经猫足够聪明,起始的时候,你至少要有 4 个子,且位置合理,才有机会捉住它。)
3、由于实际游戏中,神经猫没那么聪明,它在左上方有通道的情况下会一味地往左上方逃跑,而不会拐弯,所以,在左上防御充分的前提下,还是尽可能在其它位置做好防御,防患于未然嘛。

浏览原图
如图,正因为神经猫一开始总是往左上角跑,所以这种状态才能围住它,如果神经猫往左下或右上跑,其实是围不住的。
4、上面已经证明,当 M=9 的时候,我才能确保捉住神经猫。对于本题来说,相当比 M=5 略好一些。
故,必然存在某些情况,因为自己子力太弱,自己根本无法捉住神经猫——这个时候,就放小猫咪一个生路好了。









 粤公网安备44010602000283号
粤公网安备44010602000283号

全部评论