四千字警告!
这次内容上来说确实承接上文,也是建模,但是也和生灵身材模板那个没什么关系,是上一篇的拓展,主要针对于当时尚未解决的几个发展方向做出一些小小的研究。
(原先的生灵身材模板还是会更新的……吧?,只是还是会鸽一些0.0)
(好吧,这话我自己说着都没信心hhhh)
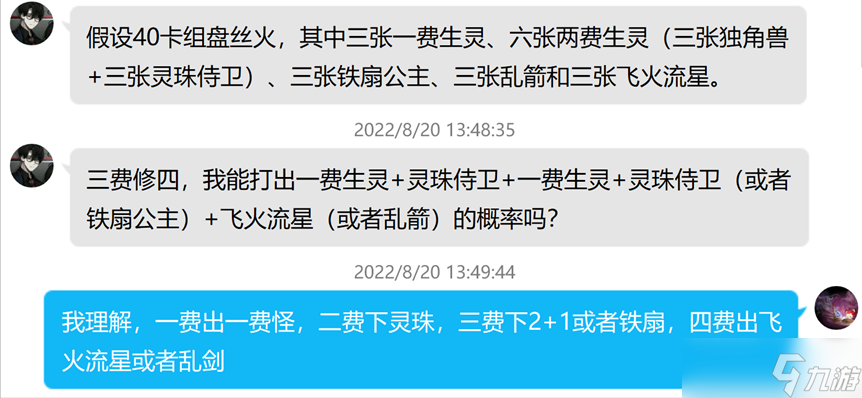
好了,在看今天的正题之前,我们先来看一下十几天前我新接的私活:

当然条件给错了,实际是九张一费生灵,不过这无伤大雅,只是参数上的改变罢了。
那么我们来严肃的思考下这个问题,上文我们解决了单核心卡的开局上手率问题,而这次的私活本质上是多核心卡在特定回合前上手率的问题,这就需要我们解决上次留下来的三个小尾巴:

这也就是我们今天的正题:多核心卡在过牌期望内的上手率模拟。
(说是模拟好像有些不太恰当,更准确的说应该是仿真,也就是造假hhhh)
原先的假设就不多谈了,有兴趣的话可以翻一下,那么根据原先的小尾巴,我们按解决顺序提出一些基本的假设:
1. 后续抽牌不考虑如【斜月秘技】、【袁天罡】这种非常规的随机抽牌。仅以能被触发惊变的标准作为后续的抽牌模拟。
2. 多种核心卡的同时上手率问题,在某种核心卡手上超量的情况下可以予以换掉,比如说要算ABCD四种核心卡的上手率问题,后手可以换三张,手里有ABCABC,需要换其中三张ABC去找D。同时不考虑先手核心卡种类超过五张,后手换核心卡种类超过四张的情况,这也就保证开局一定会换牌并换满先后手的二三张。
(不过一般卡组核心卡也很难超过四种吧……)
3. 核心卡不单指一张卡,可适用于同定位卡,比如九张一费怪可以算作A类核心卡,六张二费怪可以算作B类核心卡,这时A类核心卡的数量就是9,B类就是6,不一定指满编最多三张的单卡。
柿子捡软的捏,我们先来解决比较简单的尾巴2,也就是单核心卡在特定回合前的上手率问题吧。
在假设1的条件下,我们实际就可以把整个对局中的手牌分成两个阶段,开局换牌阶段与后续抽牌阶段。
开局换牌阶段的计算方法我就不多赘述了,有兴趣的话可以参考。
而这个后续抽牌阶段因为不考虑非常规的随机抽牌,也就是说我们一般是能给出一个过牌期望m,m∈N+,如果m为0的话就相当于不存在后续抽牌这个阶段了。
那么此时这个后续抽牌阶段的计算就相当于在过牌期望m的一次排列组合,在牌库数量为n,核心卡数量为k,先手换牌情况下至少上手一张核心卡为事件B1,可得:

嗯……可能公式看起来有点复杂,但原理还是很简单的吧?
至于正向计算事件B1,则会变得比较复杂,需要分别计算正好一张核心卡的情况(也就是事件B2),正好两张核心卡的情况,正好三张核心卡的情况……这里的计算量就会爆炸增长,我们需要尽量避免这种令人头痛的事情发生。
也就是说,单核心卡在特定回合前上手率的问题我们已经简化成了以过牌期望的形式进行分步排列组合解决,同理可以根据上次的帖子算出来过牌期望为m的情况下至少x张核心卡上手率,这个原理是一样的,只是原先的一次排列组合变成了两次,我就不多赘述了。
那么带入具体数据,我们可以算出来40张牌库,【百鬼夜行·稀】数量为3,在三跳四修的回合过牌期望为5的情况下,四费能准时打出百鬼的概率:
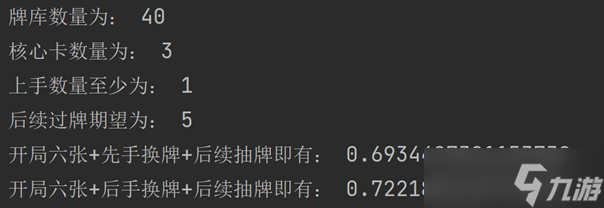
(这里的后续过牌数量是算回合自动抽牌的,也就是说先手在三跳四修回合会总共自动抽到3张牌,这期间再抽两张牌就达到了5的期望,如果是后手,那只用再额外抽一张牌就够了,对于土系来说应该还是比较简单的吧?)
小尾巴2,解决。
事实上两次排列组合是不是感觉还是比较麻烦?至少对于多种核心卡的多张上手率来说,分类讨论的数量直接指数增长,那么有没有简单些的近似计算呢?
(当然这里指的不是求导或者泰勒那种的近似计算hhhh)
能否将两次排列组合换成一次呢?
思考一下,如果开局完全不换牌的话,那么其实整体就是一个排列组合,相当于不断从卡牌数量为n的牌库中进行一次次不放回的抽牌,只是换牌的这个动作使得有两次抽牌放回了,去掉这两次的话这完全可以简化为一次简单的排列组合。

当然,这会造成一定的误差,毕竟先手情况一个是n张牌进行6次不放回抽牌和2次放回抽牌,一个是n+2张牌中进行8次不放回抽牌,误差是肯定存在的,近似计算结果会比精确算出来的概率要小一点点。
我们带入具体数据看看,在40张牌库中核心卡数量为3,上手至少一张的概率用精确方法和近似方法算一下:

是不是感觉还能接受?而且这里还是影响最大的开局换牌部分,如果有后续抽牌部分的话两种结果会更为接近一些。
小尾巴3,解决。
那么最后就是多核心卡的上手率问题。
首先我们来看一个错误的例子:
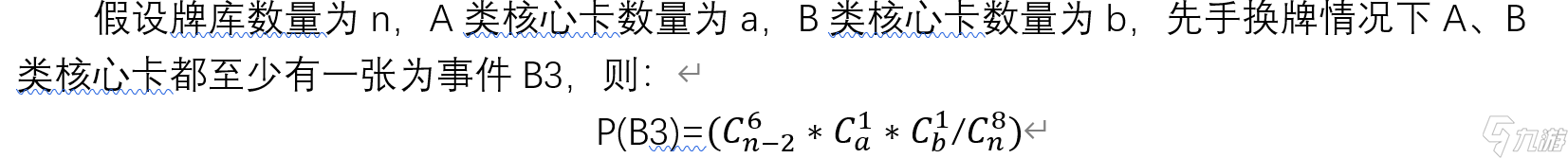
近似计算的话就相当于和n相关的都变成n+2就行,后手就是n+3。
我们带入具体值,牌库数量为40,【定海神珠】数量为3,【平等王】数量为3,开局手上有珠子且有平等的概率就是:

看上去是不是很合理?
然而这里实际有涉及重复计算某些特殊的情况。
我们来看另一个实际问题,看完这个大致就明白了:


当m=0时,算的就是开局六张+换牌两张的A、B两类核心卡上手概率,不考虑后续抽牌阶段,这里是算的精确值,如果是后手,将所有8改为9即可。
当m>0时,算的就是加上后续抽牌期望为m,这里因为两次排列组合分类讨论较为复杂,只能用近似方式计算,先手将所有n改为n+2即可,后手将所有8改为9,n改为n+3即可。
带入具体值吧,牌库数量为40,【定海神珠】数量为3,【平等王】数量为3,开局手上有珠子有平等的概率就是:

近似计算的误差在10%左右,还可以接受的吧?
至于能否直接近似成单核心卡上手率幂的形式……由于篇幅原因我就不细说了,结论是在多种核心卡数量相等且其和不超过6+m的过牌期望时是可以的,具体效果还不错,会比精确值稍高一点点,但误差和近似计算差不太多,后手这方面甚至更好一些,但就是条件局限性比较大,两个条件一旦不满足其一结果都会有较为明显的误差。
小尾巴1,解决。
好的,那么我们终于可以开始着手解决一开头的私活了,想不到就这么过去了一周多的时间……
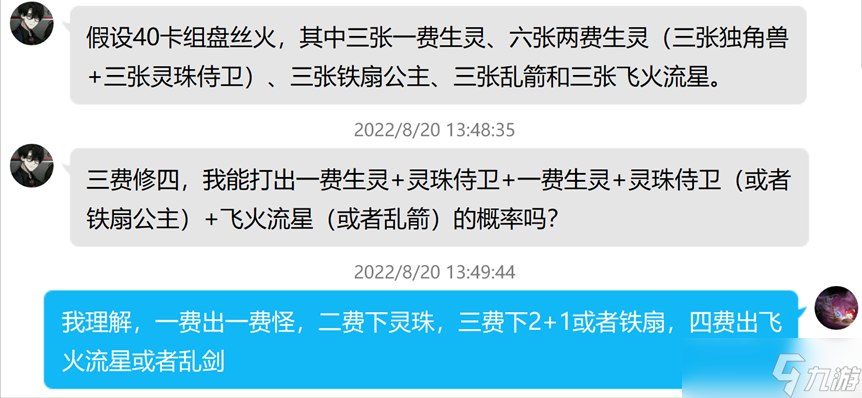
这里我们适当简化一下问题,将核心卡归纳为4种,一费生灵为A类共计9张,二费生灵为B类(这里我们先将独角兽等价为灵珠,后续再进行处理)共计6张,铁扇公主为C类共计3张,乱剑和飞火流星为D类共计6张。
盘丝火本身是没有过牌卡的,前期要铺场也不会用门派技能,那么在三跳四这个回合先手过牌数量就为3,后手就为4,这里是很确定的,甚至用不上期望这个词。
因为三费本身可选情况有两种,我们就要分类讨论出两种情况:
第一种是在三费下铁扇公主,这就相当于手牌中A类核心卡1张,B类核心卡一张,C类核心卡一张,D类核心卡一张。
(因为3费出铁扇,所以2费出灵珠和独角兽差别都不大了,灵珠也享受不到收益的,就都归为B类好了)
第二种是在三费2+1,这就相当于A类核心卡两张,B类核心卡两张,C类核心卡0张,D类核心卡一张。
(注意这里C类一定是0张,不然根据加法原理与第一种有重复计算部分)
当然呢这里我们与原问题有一些出入,首先是不能保证牌序的问题,比如同样是ABCD各一张,但是三跳四修那个回合一费怪才来,肯定是与实际情况不符,但是在这个模型当中会被纳入可行解(记为第一个偏高情况)。还有就是第二种情况中没有排除掉B类核心卡上手的全是独角兽(记为第二个偏高情况),所以实际计算值我个人认为会偏高一些。
那么带入具体值进行计算,可得:

我们将这个结果记为P(H),将真实概率记为P(T),将以下情况带来的结果记为P(L):
B类核心卡数量变更为4,删去两张独角兽,这样能保证第一种情况下铁扇时灵珠与独角兽同样没差,但第二种情况只要上手两张核心卡,就一定会有至少一张灵珠。
这么做的话能保证原先两个偏高情况中的第二个被纠正了,但是也因为核心卡数量与实际不符,会导致结果明显偏低。
让我们代入具体值计算一下:

这里我们也能初步得出一个结论:
P(H)> P(T)> P(L)。
事实上还有一种方法进行近似,就是将B类核心卡数量改为5,这样第二个偏高情况只有正好上手两张B类核心卡且均为独角兽才会属于不符合实际但被纳入可行解的范围,这个概率是非常小的,将这个结果记为P(S),我个人觉得P(S)会更接近于真实概率P(T):
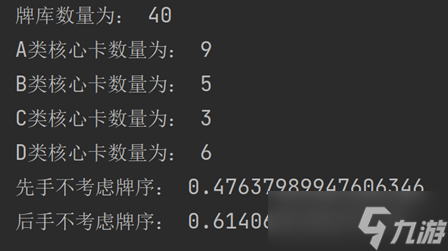
至于考虑到牌序带来的影响会比较复杂,可以用随机数模拟序列的方式来求精确解,但我这里还是决定根据上下限和个人经验给出一定的近似值(主要还是拖太久了,赶紧解决了吧hhhh)。
第一个偏高情况是由牌序引起的问题,砍期望能保证某卡在提前几个回合上手,但是砍期望也就意味着默认少抽了一次牌,会使得总体结果继续下降,而且下降量很多,我脑测一下在有9张一费和6张二费的情况下,一二三费完全倒序来牌概率不大,所以我个人认为期望为2的会比较接近真实概率P(T),同时带入核心卡数量为6计算一下:

和之前的P(S)差不太多,对于本来抽牌数量就少还少换一张的先手来说砍一点期望会比后手影响更大一些,正常。
所以综上所述,我们得出结论:
打出如此combo的先手概率大致在0.45附近,后手概率在0.6附近。
好的!那么到止为止本次水帖的正文部分已经基本结束了,我们来总结一下具体做了些什么吧:
1. 单核心卡在特定回合前的上手率通过过牌期望的形式解决了问题。
2. 开局换牌阶段和后续抽牌阶段统一简化为一次排列组合进行近似计算。
3. 多核心卡的核心上手率使用排列组合的加法原理解决了问题。
4. 综合利用上面三种方法解决实际私活提出的问题,并不严谨,还有提升空间,但是个人觉得误差不大(意思就是懒得再做了hhhh)
那么在这里其实绝大多数上手率问题都能通过这个框架来进行解决了,但我们还是有一些小尾巴没有收尾(怎么这么多尾巴0.0),算是做下一次的更新预告了:
1. 正向计算和反向计算值其实是不一样的,换牌也有独有的海崖式算法。


2. 马三刑三还是马二刑三还是马三刑二?基于马刑问题的上手率模拟与构筑研究。
3. 潜龙出海的生灵结算优先级真的是从左到右吗?为什么感觉傀儡师总是第一个触发?
(好吧,第三个问题应该不在下一期的【卡牌建模计划】更新中,应该算是水晶的【机制讲堂】或者【bug讲堂】里面的,凑个数吧。短时间内预计还会有一个和韦师傅联合开发的因缘卡组攻略更新)
怎么感觉每次解决了一个问题,就冒出了更多的更复杂的问题……
可恶,下机!









 粤公网安备44010602000283号
粤公网安备44010602000283号

全部评论