-
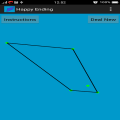
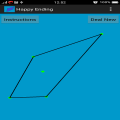
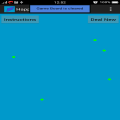
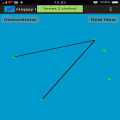
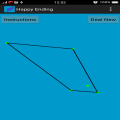
幸福结局问题! 美的享受和神秘感的随机性,概率几何! 五个绿点被随意放置在屏幕上。 这些点在屏幕的不同区域随机生成的。 假设所有的5点不是在一条线上,并且点相互分离,这样就可以区分点和点击这些。 你应该总是能够连接他们四人创建一个凸四边形,这与四边,所有的角落都小于180度的形状。 按照维基百科: “A凸...
Happy Ending Problem

幸福结局问题! 美的享受和神秘感的随机性,概率几何! 五个绿点被随意放置在屏幕上。 这些点在屏幕的不同区域随机生成的。 假设所有的5点不是在一条线上,并且点相互分离,这样就可以区分点和点击这些。 你应该总是能够连接他们四人创建一个凸四边形,这与四边,所有的角落都小于180度的形状。 按照维基百科: “A凸多边形是一个简单的多边形(未自相交),其中边界上的两个点之间没有线段过去的多边形之外。等效地,它是一个简单的多边形,其内部是一个凸集。 在一个凸多边形,所有内角都小于或等于180度,而在严格的凸多边形的所有内角都严格小于180度“。 定理的寓意是,你永远是能够创造一个凸四边形与五个胡乱点,无论在哪里,这些点被定位。 这个故事的寓意是,它是如何工作的四个侧面。 但是,对于一个五边形,9点是required.For六边形,需要17点。 但除此之外,我们仍然不知道。 这是一个谜许多点都是如何才能创建一个七边形或任何较大的形状。 可能有一个公式来告诉我们有多少点所需的任何形状。 数学家怀疑方程为M = 1 + 2 ^(N - 2),其中M是点的数量,而N是边在形状数。这里^表示功率。 这个简单的游戏,只有5个点即用于一凸四边形的情况下的交易。 这个游戏可以运行在某些设备上缓慢。 BUG: ***在指令式被错误地写为M = 1 + 2N-2而不是M = 1 + 2 ^(N-2)。 此游戏是完全免费的,有NO-ADS或没有应用内购买。 ***在任何错误或任何错误信息的情况下,请给我发电子邮件。
Happy Ending Problem游戏截图
新游排行榜
新游期待榜
热门推荐
相关专题
最新专题
- 背包战争福西法的宝藏下载速度慢什么原因
- 下载现代战舰最新版地址介绍
- 坦克大战之终极之战下载
- 决策三国下载链接
- 动物栏桌面牧场下载渠道
- 经典的二战坦克游戏top5
- 日本乙女游戏都有哪些
- 耐玩的2战游戏大全2025
- 2025飞机大战游戏有哪些
- 人气较高的80后游戏排行榜
- 悖论之门下载速度慢为什么
- 杯杯倒满下载速度慢怎么办
- 西瓜派对下载渠道有哪些
- 沙滩大作战下载渠道有哪些
- 望月预约地址哪个好
- 守卫与远征下载链接分享
- 小黄鸭模拟器下载地址介绍
- 消灭方块下载链接详解
- 好玩的3d动作网络游戏下载合集
- 经典的手游生存游戏下载推荐
- 耐玩的音乐小游戏有哪些
- 关于火的手游下载推荐
- 热门的喜羊羊游戏闯关游戏推荐
- 人气较高的修仙单机手游推荐
- 好玩的换装手游排行榜
- 好玩的3d格斗手机游戏排行榜
- 运动会可以玩的游戏有哪些2023
- 主播玩的最热门的游戏有哪些
- 有趣的3d动作游戏好玩的有哪些
- 一个勇士救公主的老游戏叫什么
- 友情链接
- 最新游戏
























 粤公网安备44010602000283号
粤公网安备44010602000283号

玩家评论
更多>>全部评论